Question

In ΔHIJ, the measure of ∠J=90°, JI = 4, HJ = 3, and IH = 5. What ratio represents the tangent of ∠I?

Answer 1

3/4

Explanation:

Answer 2

The ratio
`(3)/(4)` represents the tangent of ∠I

Explanation:

Let us revise the trigonometry ratio

• sin Ф =
  `(opposite)/(hypotenuse)`
• cos Ф =
  `(adjacent)/(hypotenuse)`
• tan Ф =
  `(opposite)/(adjacent)`

In Δ HIJ

∵ m∠J = 90°

- Hypotenuse is the side which opposite to the right angle

∴ HI is the hypotenuse

∵ HJ = 3 units

∵ IH = 5 units

- Let us use Pythagoras Theorem to find HJ

∵ (HJ)² + (IJ)² = (IH)²

∴ 3² + (IJ)² = 5²

∴ 9 + (IJ)² = 25

- Subtract 9 from both sides

∴ (IJ)² = 16

- take √ for both sides

∴ IJ = 4 units

To find the tangent of ∠I find the opposite and adjacent sides to it

∵ HJ is opposite to ∠I

∵ IJ is adjacent to ∠I

- use the rule of tan above

∴ tan(∠I) =
`(HJ)/(IJ)`

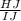
∴ tan(∠I) =
`(3)/(4)`

The ratio
`(3)/(4)` represents the tangent of ∠I