Question

On circle O below, the measure of FJ is 84º . The measure of GH is 76°.
What is the measure of

Answer 1

Given:

Measure of arc FJ = 84°

Measure of arc GH = 76°

To find:

The measure of angle HKJ.

Solution:

The image of the question is attached below.

Angles inside the circle theorem:

If two chords intersect inside a circle, then the measure of each angle is one half the sum of the measures of the intercepted arc and its vertical arc.

`$\Rightarrow m \angle G K H=(1)/(2)(m(a r \ G H)+m(a r \ F J))`

`$\Rightarrow m \angle G K H=(1)/(2)\left(76^(\circ)+84^(\circ)\right)`

`$\Rightarrow m \angle G K H=(1)/(2)\left(160^(\circ)\right)`

`\Rightarrow m \angle G K H=80^(\circ)`

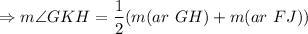
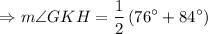
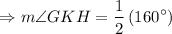
Sum of the adjacent angles in a straight line is 180°.

⇒ m∠GKH + m∠HKJ = 180°

⇒ 80° + m∠HKJ = 180°

Subtract 80° from both sides.

⇒ 80° + m∠HKJ - 80° = 180° - 80°

⇒ m∠HKJ = 100°

The measure of ∠HKJ is 100°.