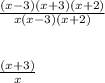Question

Simplify this equation...

Answer 1

Answer: 3)
`(x+3)/(x)`

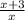
Explanation:

Start by factoring the numerator by grouping

`(x^3+2x^2-9x-18)/(x^3-x^2-6x) \\((x^3+2x^2)+(-9x-18))/(x^3-x^2-6x) \\(x^2(x+2)-9(x+2))/(x^3-x^2-6x) \\((x^2-9)(x+2))/(x^3-x^2-6x) \\((x-3)(x+3)(x+2))/(x^3-x^2-6x)`

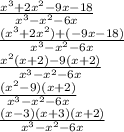
Now factor the denominator

`\\((x-3)(x+3)(x+2))/(x^3-x^2-6x)\\ \\((x-3)(x+3)(x+2))/(x(x^2-x-6))\\`

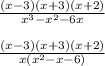
Factor the trinomials by finding two numbers that add to get -1 and multiply to get -6. In this case the numbers are -3 and 2

`\\((x-3)(x+3)(x+2))/(x(x^2-x-6))\\\\\\((x-3)(x+3)(x+2))/(x(x-3)(x+2))\\`

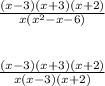
Cancel out the terms that are both in the numerator and denominator. In this case they are (x-3) and (x+2)

`\\((x-3)(x+3)(x+2))/(x(x-3)(x+2))\\\\\\((x+3))/(x)\\`