Question

Select the correct answer from each drop down menu a= 1/10, -10, 1/50, -1/10 b= i/10, -10i, -1/10, -i/50

Answer 1

Given:

`$(2 i)/(2+i)-(3 i)/(3+i)=a+b i`

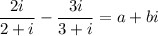
To find:

The value of a and b.

Solution:

`$(2 i)/(2+i)-(3 i)/(3+i)`

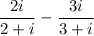
LCM of
`2+i, 3+i=(2+i)(3+i)`

Make the denominator as LCM.

`$=(2 i(3+i))/((2+i)(3+i))-(3 i(2+i))/((3+i)(2+i))`

`$=(2 i(3+i)-3 i(2+i))/((2+i)(3+i))`

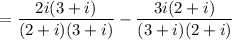
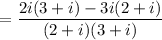
Multiply the common term into inside the bracket.

`$=(6i+2i^2-6i-3i^2)/(6+2i+3i+i^2)`

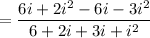
The value of i² = -1

`$=(6i-2-6i+3)/(6+2i+3i-1)`

`$=(1)/(5+5i)`

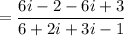
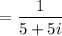
Rationalize the denominator:

Multiply the conjugate.

`$=(1)/(5+5i)* (5-5i)/(5-5i)`

`$=(5-5i)/(5^2-(5i)^2)`

`$=(5-5i)/(50)`

`$=(5)/(50)-(5i)/(50)`

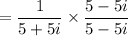
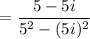
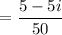
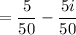
Cancelling the common factors, we get

`$=(1)/(10)-(1)/(10) i`

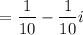
The value of a is
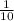`(1)/(10)` and the value of b is
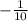`-(1)/(10)`.