Question

Please help with this I'm kinda cheeks when it comes to math

Answer 1

We're choosing among

`y = \pm 4^(\pm x)`

and we have to figure out which signs goes with which graph.

If they're both positive we have a pretty normal exponential,

`y = 4^x`

That's going to be zero as x gets negative and exponentially explode toward positive infinity for positive x. Graph 3.

`y = -4^x`

That's the same as the last one except it goes to negative infinity. It's the last one reflected in the x axis. Graph 4.

`y = (\frac 1 4)^x`

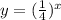
When we have a fraction between 0 and 1 for the base as x gets bigger this goes to zero and as x gets more negative, this diverges toward positive infinity. It's our first graph reflected in the y axis, the same as
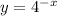`y=4^(-x)`. That's our first graph reflected in the y axis. Graph 1.

`y = (-\frac 1 4)^x`

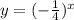
That's the same as
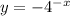`y=-4^(-x)`. As x gets more negative y diverges toward negative infinity. Graph 2.

Answer 2

graph 2: f(x) = -(1/4)^x

graph 3: g(x) = 4^x

graph 1: k(x) = (1/4)^x

graph 4: h(x) = -4^x

i feel that, math sucks