Question

Rocket is launched from a tower. The height of the rocket, y in feet, is related to the time after launch, x in seconds, by the given equation. Using this equation, find the time that the rocket will hit the ground, to the nearest 100th of second.

y=-16x^2+199x+90

Answer 1

The time that the rocket will hit the ground is 12.87 seconds.

Explanation:

Given : The rocket is launched from a tower
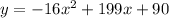`y=-16x^2+199x+90`. The height of the rocket, y in feet, is related to the time after launch, x in seconds, by the given equation.

To find : The time that the rocket will hit the ground ?

Solution :

When the rocket hit the ground i.e. height became zero y=0,

Equation is
`y=-16x^2+199x+90`

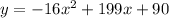
Substitute y=0,

`-16x^2+199x+90=0`

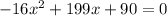
Using quadratic formula,
`x=(-b\pm√(b^2-4ac))/(2a)`

`x=(-(199)\pm√((199)^2-4(-16)(90)))/(2(-16))`

`x=(-199\pm√(45361))/(-32)`

`x=(-199+√(45361))/(-32),(-199-√(45361))/(-32)`

`x=-0.43,12.87`

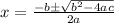
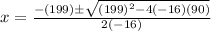
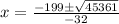
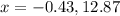
Reject negative value.

The time taken is 12.87 seconds.