Question

1. You are driving along a highway at 35.0 m/s when you hear the siren of a police car approaching you at 44.2 m/s from behind and you perceive the frequency as 1310 Hz. You are relieved that he is in pursuit of a different speeder when he continues past you, but now you perceive the frequency as 1240 Hz. What is the frequency of the siren in the police car

Answer 1

The frequency of the siren in the police car is 1270.45 Hz

Step-by-step explanation:

Here we have

`f_d = f(v-v_r)/(v-v_s)`

`f = f_d(v-v_s)/(v-v_r) = 1310(v-44.2)/(v-35)`

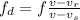
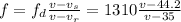
f(v-35) = 1310(v-44.2)

fv -35f = 1310v - 57902....(1)

Also

`f_d = f(v+v_r)/(v+v_s)`

`f = f_d(v+v_s)/(v+v_r)`

`f = f_d(v+44.2)/(v+35)`

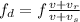
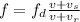
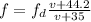
f(v + 35) = 1240(v + 44.2)

fv + 35f = 1240v + 54808.....(2)

Subtracting (1) from (2) gives

70f = 112710 -70v

Therefore f = 1610.143 -v

Substituting the value of f in (1) we get

(1610.143 -v)v -35(1610.143 -v) = 1310·v - 57902

Which gives

v²-335.143·v-1546 =0

Factorizing gives

(v + 4.554)(v - 339.697) =0

Therefore, since v is the velocity of sound, we have v = 339.697 m/s

Since our f = 1610.143 -v

f = 1610.143 -339.697 = 1270.45 Hz