Question

A solid has two bases and 5 lateral faces. What is the sum of the number of vertices and edges combined?

Answer 1

25

Explanation:

we know that

If the solid has two bases and 5 lateral faces, then the number of vertices is equal to 5 in each base

so

`Vertices=2(5)=10`

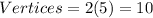
The number of edges is equal to 5 in each base plus 5 edges of the lateral faces

so

`Edges=2(5)+5=15`

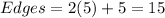
therefore

The number of vertices and edges combined is equal to

`Vertices+Edges=10+15=25`

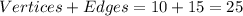
Verify

we know that

Euler’s formula for any polyhedron is given by the formula

`F+V-E=2`

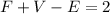
where

F is the number of faces

V is the number of vertices

E is the number of edges

we have

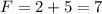`F=2+5=7` ---> 2 bases and 5 lateral faces

`V=10\\E=15`

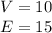
substitute

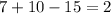`7+10-15=2` ----> is ok