Step-by-step explanation:
(a) Formula for work done in isothermal process is as follows.
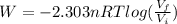
=
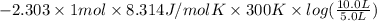
= -1729 J
And, for isothermal process
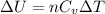
=

According to the first law of thermodynamics,
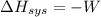
Hence,
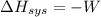 = 1729 J
= 1729 J
Also,
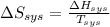
=
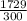
= 5.763 J/K
Here,
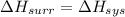 = -1729 J
= -1729 J
So,
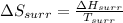
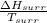 =
=
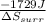
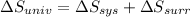
= 5.763 J/K -
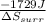
Hence, entropy changes for reversibly by adjusting the pressure of the surroundings to match the internal pressure of the gas is 5.763 J/K -
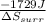 .
.
(b) Now, formula for work done in irreversible isothermal process is as follows.
W =
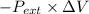
=
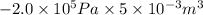
= -1000 J
For isothermal irreversible process,
 = 0
= 0
And,
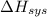 = -W + 1000 J
= -W + 1000 J
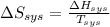
=
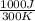
= 3.33 J/K
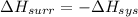 = -1000 J
= -1000 J
Therefore,
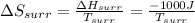
As,
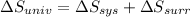
=
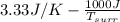
Hence, for irreversibly entropy changes freely expanding in a vacuum is
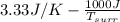 .
.