Question

Let


`Let \\ \displaystyle\sf S = \sum_(k=1)^n (n)/(n^2+kn + k^2)` and ,

`\displaystyle \sf T_n =\sum_(k=0)^(n-1)(n)/(n^2+kn+k^2)` ,
[/tex]
where n = 1,2,3,4..... Then ,

`A)\quad S_n < (\pi)/(3\sqrt3) \qquad \qquad B)\quad S_n >(\pi)/(3\sqrt3)\\\\ C)\quad T_n >(\pi)/(3\sqrt3)\qquad\qquad D)\quad T_n < (\pi)/(3\sqrt3)`
​

Answer 1

A, D

Explanation:

You want to know the bound for the values of Sn and Tn, given their definitions as ...

`\displaystyle S_n=\sum_(k=1)^n{(n)/(n^2+kn+k^2)}\\\\T_n=\sum_(k=1)^(n-1){(n)/(n^2+kn+k^2)}`

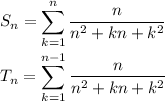
Values

All we need to do to determine the correct answer choices is evaluate the sums for some value of n.

For n=2, the value of S2 is ...

S2 = 2/(4+2+1) +2/(4+4+4) = 2/7 +2/12 = 19/42 ≈ 0.4524

For n=2, the value of T2 is ...

T2 = 2/(4+2+1) = 2/7 ≈ 0.2857 . . . . . 1/(3n) less than the value of Sn

Both of these values are less than π/(3√3) ≈ 0.6046.

The correct answer choices are ...

A) Sn < π/(3√3)

D) Tn < π/(3√3)

__

Additional comment

For the purpose here, it is not necessary to determine the limiting value of either Sn or Tn. It is only necessary to demonstrate which side of the given value the terms of either sequence lie.

<95141404393>