Question

an insect population grows at a rate of 25% per year.if its initial population is 4.2 million what will be its population in three year?

Answer 1

The population after 3 years would be 8.20 millions.

Explanation:

Given,

Initial population = I = 4.2 million

Growing rate = r = 25%

If the initial population and growing rate is given, the formula to calculate the population (x) after n years would be:

`x = I * (1 + (r)/(100) )^(n)`

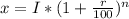
By putting the values in the equation, we get

`x = 4.2 * (1 + (25)/(100) )^(n)`

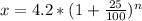
The population after 1st year (x1) would be

`x1 = 4.2 * (1 + (25)/(100) )^(1)`

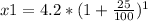
x1 = 5.25 million

Similarly,

`x2 = 4.2 * (1 + (25)/(100) )^(2)`

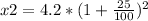
x2 = 6.56 million

`x3 = 4.2 * (1 + (25)/(100) )^(3)`

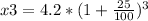
x3 = 8.20 million

Hence, the population after 3 years would be 8.20 millions.

But, if you are asking about the total population at that time. It would be

I + x1 + x2 + x3 = 24.21 million