Answer:
The z-value rounded to the nearest hundredth is -1.64
There is no enough evidence to reject the claim.
Explanation:
A certain website claims that it averages 4.7 hours of downtime per month.
No. of samples = n = 17
Mean =
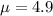
Standard deviation =
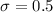
Formula:
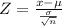
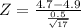
Z =−1.64
Z critical at 90% is 1.65
Since Z calculated < Z critical
So, there is no enough evidence to reject the claim.