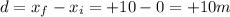a) 20 metres
b) +20 metres
c) 30 metres
d) +10 metres
Step-by-step explanation:
a)
Distance is a scalar quantity which represents the total length of the path covered by an object in motion.
Displacement, instead, is a vector quantity connecting the initial position to the final position of motion of the object.
In this problem:
- The length of the room is 20 metres
- Jasmin walked from the back of the room to the front of the room
Therefore, the total length of the path covered by Jasmine is equal to the length of the room, therefore it is:
d = L = 20 metres
b)
As we said before, displacement is a vector connecting the initial position of motion to the final position of motion.
Here we can choose the origin (position zero) as the back of the room, so that

is the initial position.
Then, Jasmine walked 20 metres towards the front; so her final position is
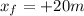
Therefore, the displacement is the difference between the initial and final position; it is:
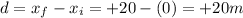
c)
Here Jasmine walks half way back.
This means that the total distance covered by Jasmine is:
- The full length of the room (to reach the front)
+
- Half length of the room (to come back half way)
So the total distance covered is:
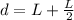
where
L = 20 m is the length of the room
Substituting, we find the total distance:

d)
Here Jasmine walks half way back.
So we have to compute her new displacement.
In this situation, we have:

is the initial position, since she started from the back of the room
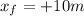
is her final position, since she walked halfway back, so the reaches half of the room as her final position
Therefore, the displacement of Jasmine in this case is: