Question

Seventeen concert tickets were sold for $550. Each adult ticket costs $9 and each children's ticket costs $5 find the number of adult tickets and the number of children's tickets sold

Answer 1

The number of adult's ticket is 50.

The number of children's ticket is 20.

Explanation:

Given that, seventy ticket were sold for $550.

Let the number of adult's ticket be x.

Then the number of children's tickets is = (70-x)

Each adult ticket cost $9.

Then the cost of x number of adult's ticket is = $9x

Each children's ticket cost $5

Then the cost of (17-x) number of children's ticket is=$5(70-x)

=$(350-5x)

According to the problem,

`9x+(350-5x)=550`

`\Rightarrow 4x+350=550`

`\Rightarrow 4x=550-350`

`\Rightarrow 4x=200`

`\Rightarrow x=(200)/(4)`

`\Rightarrow x=50`

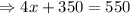
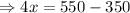
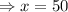
The number of adult's ticket is 50.

The number of children's ticket is (70-50)=20