Answer:
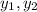 satisfies given homogenous solution and the particular solution is
satisfies given homogenous solution and the particular solution is
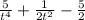 .
.
Explanation:
Given homogeneous equation is,
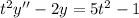 where t>0 subject to
where t>0 subject to

To verify,
- wheather
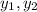 satisfies given homogenous equation, then both will satisfy
satisfies given homogenous equation, then both will satisfy
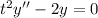 that is,
that is,
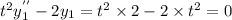
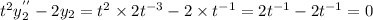
Thus
 and
and
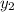 satisfies (1).
satisfies (1).
Now the wronskean,
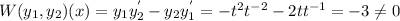
Thus
 and
and
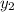 are solution of (1) .
are solution of (1) .
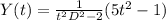 where
where
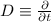
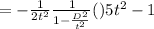
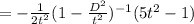
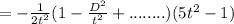
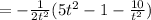 sincce
sincce
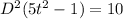
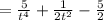
Hence the result.