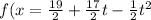Answer:
Therefore the quadratic function is
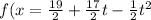
Explanation:
We want find a quadratic function
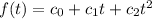
such that, f(0)=10, f(1)=16, f(2)=26, f(3)=30
These conditions gives the following system of linear equations
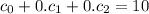
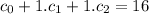
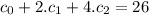
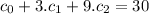
Let
![A=\left[\begin{array}{ccc}1&0&0\\1&1&1\\1&2&4\\1&3&9\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/u1zs8jkurdvvu88f49b792n0uqwo5ke1d7.png) ,
,
![\vec x= \left[\begin{array}{c}c_0\\c_1\\c_2\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/um11h5wemxvt7y8o2rjff1u2kr1p25e07x.png) and
and
![\vec b=\left[\begin{array}{ccc}10\\16\\26\\30\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/b4x1aiyyn1qeqcs4r5qq6glusyajqvmr60.png)
The unique least square solution is
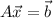
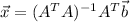
![\left[\begin{array}{c}c_0\\c_1\\c_2\end{array}\right]=\left(\left[\begin{array}{cccc}1&1&1&1\\0&1&2&3\\0&1&4&9\end{array}\right] \left[\begin{array}{ccc}1&0&0\\1&1&1\\1&2&4\\1&3&9\end{array}\right]\right)^(-1)\left[\begin{array}{cccc}1&1&1&1\\0&1&2&3\\0&1&4&9\end{array}\right]\left[\begin{array}{ccc}10\\16\\26\\30\end{array}\right]]()
![\left[\begin{array}{c}c_0\\c_1\\c_2\end{array}\right]=\left(\left[\begin{array}{ccc}4&6&14\\6&14&36\\14&36&98\end{array}\right] \right)^(-1)\left[\begin{array}{cccc}1&1&1&1\\0&1&2&3\\0&1&4&9\end{array}\right] \left[\begin{array}{ccc}10\\16\\26\\30\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/804ggyl7xfh7tksye4xpslxs7gon1elvxh.png)
![\left[\begin{array}{c}c_0\\c_1\\c_2\end{array}\right]=\left[\begin{array}{ccc}(19)/(20)&-(21)/(20)&\frac14 \\ \\-(21)/(20)&(49)/(20)&-(3)/(4)\\ \\ \frac14&-\frac34& \frac14 \end{array}\right] \left[\begin{array}{cccc}1&1&1&1\\0&1&2&3\\0&1&4&9\end{array}\right] \left[\begin{array}{ccc}10\\16\\26\\30\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/y1x3gq257uicx7nih432giy9eeh5vgsk91.png)
![\left[\begin{array}{c}c_0\\c_1\\c_2\end{array}\right]= \left[\begin{array}{c}(19)/(2)\\ \\(17)/(2)\\ \\-\frac12\end{array}\right]](https://img.qammunity.org/2021/formulas/mathematics/college/pcfjm49poei6qslwbmi1rxbp6b4foes4ym.png)
Therefore
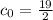 ,
,
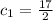 and
and
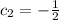 .
.
Therefore the quadratic function is