Answer:
r = - 1 or r = 1/2
Explanation:
From the quadratic equation;
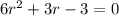
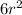 + 6r - 3r - 3 = 0
+ 6r - 3r - 3 = 0
(
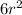 + 6r) - (3r + 3) = 0
+ 6r) - (3r + 3) = 0
6r(r + 1) - 3 (r + 1) = 0
⇒ (r + 1) or (6r - 3) = 0
r + 1 = 0 or 6r - 3 = 0
r = - 1 or 6r = 3
r = - 1 or r = 1/2
Thus, the solutions to the equation are; r = - 1 or r = 1/2 since erx is never 0.