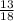Question

Suppose that of 900 pints of ice cream for sale, 200 are sugarless, 500 are vanilla, and 50 sugarless vanilla. What is the probability that a pint selected at random is either sugarless or vanilla? Simplify the fraction. Group of answer choices 5/6 13/18 7/9

Answer 1

The probability that a pint selected at random is either sugarless or vanilla is
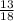`(13)/(18)` ⇒ 2nd answer

Explanation:

If A and B are to events, then

P(A or B) = P(A) + P(B) - P(A and B)

Probability of an event =
`(n(event))/(n(total))`

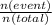
∵ There are 900 pints of ice-cream for sale

∴ n(total) = 900

∵ 200 are sugarless

∴ n(sugarless) = 200

- Divide n(sugarless) by n(total) to find P(sugarless)

∴ P(sugarless) =
`(200)/(900)`

∴ P(sugarless) =
`(2)/(9)`

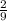
∵ 500 are vanilla

∴ n(vanilla) = 500

- Divide n(vanilla) by n(total) to find P(sugarless)

∴ P(vanilla) =
`(500)/(900)`

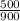
∴ P(vanilla) =
`(5)/(9)`

∵ There are 50 sugarless vanilla

∴ n(sugarless and vanilla) = 50

- Divide n(sugarless and vanilla) by n(total) to find P(s and v)

∴ P(s and v) =
`(50)/(900)`

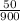
∴ P(s and v) =
`(5)/(90)`

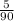
Let us use the rule above to find P(s or v)

∵ P(s or v) = P(s) + P(v) - P(s and v)

∴ P(s or v) =
`(2)/(9)+(5)/(9)-(5)/(90)`

∴ P(s or v) =
`(13)/(18)`

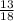
∴ P(sugarless or vanilla) is
`(13)/(18)`

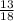
The probability that a pint selected at random is either sugarless or vanilla is
`(13)/(18)`