Answer:
Which i think is the first one, there may just be a typing error.
Explanation:
A polynomial of order n has the following format:
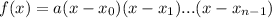
In which a is the leading coefficient,
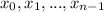 are the roots.
are the roots.
If a root appears m times, they are said to have multiplicity m.
Leading coefficient of 1 and roots 21 and 31 with multiplicity 1

So the correct answer is:

Which i think is the first one, there may just be a typing error.