Question

Your cell phone company Offers you a choice between two promotional deals you can either get 500 free text messages with the charge of $.10 for each text message over 500 or you can get 400 text messages with a charge of $.20 for each text message over 400 how many text messages would you have to send for the cost to be the same for either Plan?

Answer 1

The number of messages that will cost same both plans is 1000.

Explanation:

Given,

For 1st offer:

Total number of messages = 500

Charge of each message after 500 messages = $0.10

For 2nd offer:

Total number of messages = 400

Charge of each message after 400 messages = $0.20

We need to find out the number of messages can be sent for equal cost of both plans.

Solution,

Let the number of messages be 'm'.

So For 1st offer:

Total cost 'c' is equal to fixed cost for 500 messages plus charge of each message multiplied with number of messages.

framing in equation form, we get;

`c=500+0.10m`

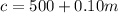
Again for 2nd offer:

Total cost 'c' is equal to fixed cost for 400 messages plus charge of each message multiplied with number of messages.

framing in equation form, we get;

`c=400+0.20m`

Now the question said that the charge would be the same.

So we can say that;

`500+0.10m=400+0.20m`

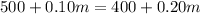
On combining the like terms, we get;

`500-400=0.20m-0.10m\\\\100=0.1m\\\\`

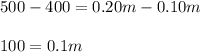
Now using multiplication property, we will multiply both side by '10' and get;

`100* 10=0.1m*10\\\\1000=m`

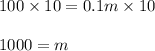
Hence The number of messages that will cost same both plans is 1000.