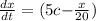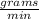Question

fish tank initially contains 35 liters of pure water. Brine of constant, but unknown, concentration of salt is flowing in at 5 liters per minute. The solution is mixed well and drained at 5 liters per minute. Let xx be the amount of salt, in grams, in the fish tank after tt minutes have elapsed. Find a formula for the rate of change in the amount of salt, dx/dtdx/dt, in terms of the amount of salt in the solution

Answer 1

Therefore, the rate of change in the amount of salt is
`(dx)/(dt) =( 5c}{ - (x )/(20))`

`(grams )/(min)`

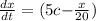
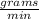
Step-by-step explanation:

Given:

Initial volume of water
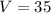`V = 35` lit

Flowing rate = 5
`(Lit)/(min)`

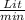
The rate of change in the amount of salt is given by,

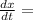`(dx)/(dt) =` ( Rate of salt enters tank - rate of sat leaves tank )

Since tank is initially filled with water so we write that,

`x(0) = 0`

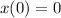
Let amount of salt in the solution is
`c`,

`(dx)/(dt) = (5c)/(1 ) - (x(t) * 5)/(100)`

`(dx)/(dt) =( 5c}{ - (x )/(20))`
`(grams)/(min)`

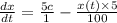
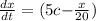
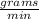
Therefore, the rate of change in the amount of salt is
`(dx)/(dt) =( 5c}{ - (x )/(20))`

`(grams )/(min)`