Question

Are the functions inverse of each other?

f(x)=5x^2+3, g(x)sqrt x-3/5

Answer 1

No.

Explanation:

Plugging in g(x) into f(x), you don't get x. g(x) would need to be =
`\sqrt{x(-3)/(5) }`

Answer 2

no

Explanation:

The function f(x) does not pass the horizontal line test, so has no inverse, except on a restricted domain. The question does not include any restriction on the domain, so the functions are not inverses of each other.

If we assume your functions are ...

`f(x)=5x^2+3\\\\g(x)=\sqrt{(x-3)/(5)}`

Then the value of g(f(x)) is ...

`g(f(x))=\sqrt{((5x^2+3)-3)/(5)}=\sqrt{(5x^2)/(5)}=√(x^2)`

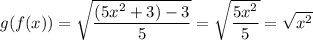
This is only equal to x when x ≥ 0. For x < 0, g(f(x)) ≠ x, so the functions are not inverses.

_____

You can see from the graph that the function g(x) is not the reflection of f(x) across the line y=x. If the functions were inverses, each would be a reflection of the other.