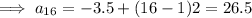Answer:
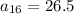
Explanation:
Arithmetic series:
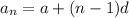
Sum of arithmetic series:
![S_n=(n)/(2)[2a+(n-1)d]](https://img.qammunity.org/2023/formulas/mathematics/high-school/3xswszu9aa97ib3vxzethlaa34iy1xjgl7.png)
(where a is the first term and d is the common difference)
Given:
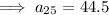
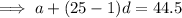
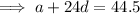
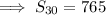
![\implies (30)/(2)[2a+(30-1)d]=765](https://img.qammunity.org/2023/formulas/mathematics/high-school/sshecntjr0v1fi0f4a85xy5t7wd9letn91.png)

Rewrite
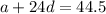 to make a the subject:
to make a the subject:
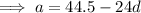
Substitute found expression for a into
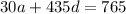 and solve for d:
and solve for d:
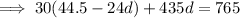
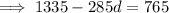
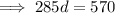
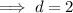
Substitute found value of d into
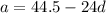 and solve for a:
and solve for a:

Therefore: