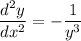Question

Find the second derivative of the parametric equation x(t)=sin t and y(t)=cos t​

Answer 1

Presumably you mean the second derivative of y with respect to x, d²y/dx².

Compute the first derivative. By the chain rule,

`(dy)/(dx) = (dy)/(dt) * (dt)/(dx) = ((dy)/(dt))/((dx)/(dt))`

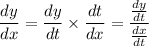
Differentiate the two parametric equations with respect to t :

`x = \sin(t) \implies (dx)/(dt) = \cos(t)`

`y = \cos(t) \implies (dy)/(dt) = -\sin(t)`

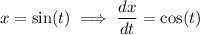
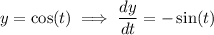
Then the first derivative is

`(dy)/(dx) = (-\sin(t))/(\cos(t)) = -\tan(t)`

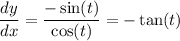
Now, dy/dx is a function of t, so we can denote it by, say, dy/dx = f(t). Then by the chain rule, the second derivative will be

`(d^2y)/(dx^2) = (df)/(dx) = (df)/(dt) * (dt)/(dx) = ((df)/(dt))/((dx)/(dt))`

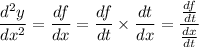
Differentiating f(t) :

`f(t) = -\tan(t) \implies (df)/(dt) = -\sec^2(t)`

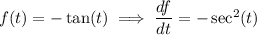
Then the second derivative is

`(d^2y)/(dx^2) = (-\sec^2(t))/(\cos(t)) = \boxed{-\sec^3(t)}`

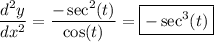
and since y = cos(t), we can go on to say

`(d^2y)/(dx^2) = -\frac1{y^3}`