Given that the radius of the circle is 6 cm.
The central angle is 120°
We need to determine the length of AB.
Length of AB:
The length of AB can be determined using the formula,
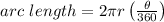
Substituting
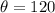 and
and
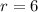 in the above formula, we get;
in the above formula, we get;
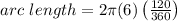
Simplifying the values, we get;
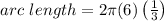
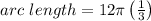
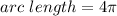
Substituting π = 3.14, we have;
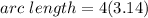
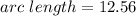
Thus, the arc length of AB is 12.56 cm