Given that Mary is three times as old as her son. In 12 years Mary will be twice as old as her son.
We need to determine the age of Mary and her son.
Let x denote the age of Mary.
Let y denote the age of her son.
Writing in the expression form of their ages, we have;
 -------(1)
-------(1)
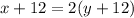 --------(2)
--------(2)
Age of Mary and her son:
Let us determine the values of x and y.
Substituting
 in the equation (2), we have;
in the equation (2), we have;
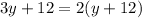

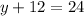

Thus, the value of y is 12.
Substituting
 in equation (1), we get;
in equation (1), we get;
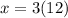
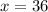
Thus, the value of x is 36.
Therefore, now the age of Mary is 36 years and her son is 12 years.