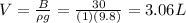Question

When a 90N rock is suspended beneath the surface of water its apparent weight is 60N. what volume of water must, therefore, be displaced?

your answer must be in numbers.
Your answer must be In liters.

Answer 1

3.06 L

Step-by-step explanation:

The apparent weight of an object floating on a liquid is given by

`W'=W-B`

where

W is the real weight of the object

B is the buoyant force, which is the upward force exerted by the fluid on the object, and its magnitude is equal to the weight of the volume of fluid displaced by the object

In this case:

W = 90 N is the real weight of the rock

W' = 60 N is the apparent weight

So the buoyant force is

`B=W-W=90-60=30 N`

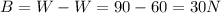
The buoyant force can be written as

`B=\rho V g`

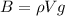
where

`\rho` is the density of the fluid

V is the volume of displaced fluid

`g=9.8 m/s^2` is the acceleration due to gravity

In this case,

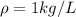`\rho = 1 kg/L` is the density of water

So, the volume of water displaced is:

`V=(B)/(\rho g)=(30)/((1)(9.8))=3.06 L`