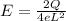Question

A Rod of length has a total charge uniformly distributed along its length. The rod lies along the axis with its center at the origin.

a. Find an expression for the electric potential as a function of position along the axis.
b. Show that the result obtained in Part (a) reduces to for Explain why this result is expected

Answer 1

a) dE={KdQdX}{r^{2} } *cosT

b) E = (2Q)/4eL^2)

Step-by-step explanation:

a) The charge of element is:

dQ = Q/L

Where the y-axis elements will cancel, thus:

`dE=(KdQdX)/(r^(2) ) *cosT`

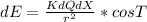
where dX is the length element = RdT and dT is the angle element, K = 1/(4pe)

b) The angle from x-axis is:

`dE=(KdQ*RdX)/(r^(2) ) *cosT`

We integrate the expression from T to p/2 and multiply by 2:

`E=(2KdQ)/(R) =(2KQ)/(LR) (2KQ_(p) )/(L^(2) )`

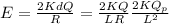
Replacing the k value:

`E=(2Q)/(4eL^(2) )`