So, we need to solve the quadratic equation from quadratic formula as per the question, but before starting, let's first recall that, for any quadratic equation of the form ax² + bc + c = 0, the discriminant is given by D = b² - 4ac, and the value of x is given by :
Also, their are no real solutions of x i.e their are only imaginary values of x iff D < 0, equal and real roots iff D = 0 and real and distinct roots iff D > 0. So, let's convert the given equation to the standard form ax² + bx + c = 0 and then we will find the discriminant and then we will be solving for k ;
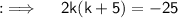
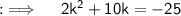
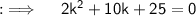
Now, on comparing this with the standard equation, we will get a = 2, b = 10 and c = 25, and then D = (10)² - 4 × 2 × 25 = 100 - 200 = - 100, now as D < 0, so their will be imaginary values of k, so now solving for k will yield by using the Quadratic Formula ;
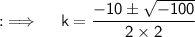
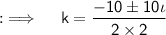
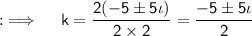
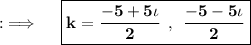
This is the required answer