Explanation:
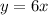
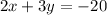
To solve this system of equations, let's multiply the first equation by
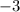 to get a
to get a
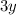 term in each equation:
term in each equation:

Now, let's add the two equations together:

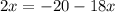
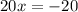
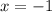
Now, we can plug in this value of
 into either equation to solve for
into either equation to solve for
 :
:
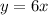
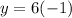
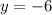
or
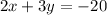
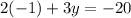
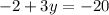
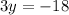
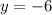
Therefore, the solution to this system of equations is
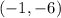 .
.