Answer:
35.
So that we have:
KLN = 54 JKN =36
LKN = 72 NMJ = 18
KNM = 126 JLM = 72
LJM = 90 KLM = 126
36.
CE = 6√13
37.
m∠Z = 88°
38.
m∠GFE = 85
Explanation:
35.
As KLMN is a kite:
+) KL = KN
=> Triangle KLN is an isosceles triangle.
=> m∠KLN = m∠ KNL = m∠KNJ = 54°
In triangle KLN, total measure of three internal angles are 180 degree, so that: m∠KLN + m∠ KNL + m∠ LKN = 180°
=> 54 + 54 + m∠ LKN = 180°
=> m∠ LKN = 180 - 54 - 54 = 72°
+) KM is the bisector of both Angle LKN and Angle LMN
So that we have:
- m∠JKN = 1/2 m∠LKN = 1/2 * 72 = 36°
- m∠NMJ = 1/2 m∠LMN = 1/2 * 36 = 18°
+) KM and LN is perpendicular to each other at point J
=> m∠LJM = 90°
+) m∠KLM = m∠KNM; m∠KLM + m∠KNM + m∠LKN + m∠LMN = 360°
=> m∠KLM + m∠KLM + 72 + 36 = 360
=> 2 m∠KLM = 360 - 72 - 36 = 252
=> m∠KLM = 252/2 = 126 = m∠KNM
+) We have: m∠KLM = m∠KLN + m∠JLM
=> m∠JLM = m∠KLM - m∠KLN = 126 - 54 = 72
36.
As BCDE is a kite, we have:
+) BC = BE; CD = DE = 21
+) BD is perpendicular to CE and intersect each other point F
=> Angle CFD = 90
=> Triangle CFD is the right triangle
According to Pythagoras theorem: CF^2 + DF^2 = CD^2
=> CF^2 = CD^2 - DF^2 = 21^2 - 18^2 = 441 - 324 = 117
=> CF =
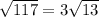
+) According to the feature of a kite shape, F is midpoint of CE
=> CF = FE = 1/2 x CE
=>CE = 2 x CF = 2 x
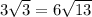
So that CE = 6√13
37.
As given, WXYZ is a kite shape.
According to the feature of a kite shape, angle ZWX and angle ZYX are equal to each other.
=> ∠ZWX = ∠ZYX
=> 8x -23 = 6x +11
=> 8x - 6x = 11 + 23
=> 2x = 34
=> x = 34/2 = 17
=> ∠ZWX = 8x - 23 = 8*17 - 23 = 113°
=> ∠ZWX = ∠ZYX = 113°
As WXYZ is a kite shape, so that total measure of 4 internal angles of it are 360 degree
So that we have:
∠Z + ∠ZWX + ∠ZYX + ∠WXY = 360
=> ∠Z + 113 + 113 + 46 = 360
=> ∠Z = 360 -113 -113-46 = 88°
So that the measure of ∠Z is 88°
38.
As GDEF is a kite shape. As we can see, GE is the longer diagonal, so that it is the bisector of both Angle DGF and Angle DEF.
H is on GE and GE is the bisector of Angle DEF, so we have:
m∠HEF = m∠GEF = 1/2. m∠DEF = 1/2 . (12x- 16)= 6x - 8
As GDEF is a kite shape so that the two diagonals DF and GE are perpendicular to each other, so that: m∠EHF = 90
In the triangle EHF, m∠EHF = 90
=> EHF is a right triangle
=> m∠HEF + m∠EFH = 90
=> 6x - 8 + 3x -1 = 90
=> 9x = 90 + 8 + 1 = 99
=> x = 99/9 =11
=> m∠HEF = 6x - 8 = 6*11 - 8 = 58 = m∠GEF
GE is the bisector of both Angle DGF
=> m∠EGF = 1/2. m∠DGF = 1/2 . 74 = 37
In the triangle GEF, total measure of three internal angles are 180
=> m∠GFE + m∠EGF + m∠GEF = 180
=> m∠GFE + 37 + 58 = 180
=> m∠GFE = 85