Question

If you weigh 685 NN on the earth, what would be your weight on the surface of a neutron star that has the same mass as our sun and a diameter of 25.0 kmkm ? Take the mass of the sun to be msmsm_s = 1.99×1030 kgkg , the gravitational constant to be GGG = 6.67×10−11 N⋅m2/kg2N⋅m2/kg2 , and the free-fall acceleration at the earth's surface to be ggg = 9.8 m/s2m/s2 .

Answer 1

`W = 5.94 \cdot 10^(15) N`

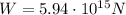
Explanation:

To calculate the weight on the surface of a neutron star we can use the following equation:

`W = m*g`

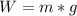
Where:

W: is the weight of the person

m: is the mass of the person

g: is the gravity of the neutron star

Hence, first we need to find m and g. The mass is equal to:

`m = (W)/(g) = (685 N)/(9.81 m/s^(2)) = 69.83 kg`

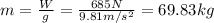
Now, the gravity of the neutron star can be found using the followig equation:

`F = (G*m*M)/(r^(2)) = m*g \rightarrow g = (G*M)/(r^(2))`

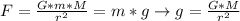
Where:

G: is the gravitational constant = 6.67x10⁻¹¹ m³ kg⁻¹ s⁻²

M: is the mass of the neutron star = 1.99x10³⁰ kg

r : is the distance between the person and the surface of the neutron star = 25/2 = 12.5 km

`g = (6.67 \cdot 10^(-11) m^(3)kg^(-1)s^(-2)*1.99 \cdot 10^(30) kg)/((12.5 \cdot 10^(3) m)^(2)) = 8.50 \cdot 10^(13) m/s^(2)`

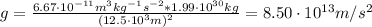
Now, we can find the weight on the surface of the neutron star:

`W = m*g = 69.83 kg * 8.50 \cdot 10^(13) m/s^(2) = 5.94 \cdot 10^(15) N`

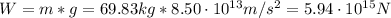
I hope it helps you!