Question

An ambulance is traveling north at 60.3 m/s, approaching a car that is also traveling north at 33.4 m/s. The ambulance driver hears his siren at a frequency of 696 Hz. Ambulance 60.3 m/s 33.4 m/s Car What is the wavelength at any position in front of the ambulance for the sound from the ambulance’s siren? The velocity of sound in air is 343 m/s. Answer in units of m.

Answer 1

0.44999 m

Step-by-step explanation:

f = Actual wavelength = 696 Hz

v = Speed of sound in air = 343 m/s

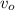`v_o` = Velocity of observer = 33.4 m/s

`v_s` = Velocity of source = 60.3 m/s

From Doppler's effect we have

`f_o=f\left((v-v_o)/(v-v_s)\right)\\\Rightarrow f_o=696\left((343-33.4)/(343-60.3)\right)\\\Rightarrow f_o=762.22709\ Hz`

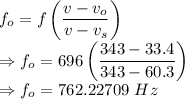
Wavelength is given by

`\lambda=(v)/(f)\\\Rightarrow \lambda=(343)/(762.22709)\\\Rightarrow \lambda=0.44999\ m`

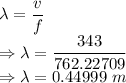
The wavelength at any position in front of the ambulance for the sound from the ambulance’s siren is 0.44999 m.