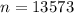Question

How many randomly selected employers must we contact in order to create an estimate in which we are 95​% confident with a margin of error of 9​%? ​b) Suppose we want to reduce the margin of error to 4​%. What sample size will​ suffice? ​c) Why might it not be worth the effort to try to get an interval with a margin of error of 1​%?

Answer 1

a)n=543

b)n=1509

c)n=13573

Explanation:

a)

c=98%,

`E=0.05`

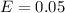
Margin Error
`E=Zα/2√p(1-p)/n`

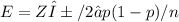
but
`n=((Zα/2)/n)²×p(1-p)`

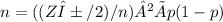
where the confidence level is 1-α=0.98

cross multiply

`Zα/2=2.33`

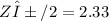
where p=0.5

input the values

`n=(2.33/0.55)²×0.5(1-0.5)=543`

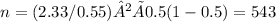
n=0.33

b) E=0.33

`E=Zα/2√p(1-p)/n`

`n=((Zα/2)/n)²×p(1-p)`

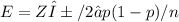
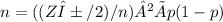
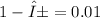`1-α=0.01` confidence level

n=(2.33/0.33)²×0.5(1-0.5)=1504

`n=1504`

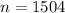
c)
`E=Zα/2√p(1-p)/n`

`n=((Zα/2)/n)²×p(1-p)`

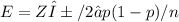
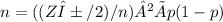
1-α=0.98

cross multiply

Zα/2=2.33

p=0.5

n=(2.33/0.01)²×0.5(1-0.5)=13573

`n=13573`