Question

Consider a short time span just before and after the spark plug in a gasoline engine ignites the fuel-air mixture and releases 1970 J of thermal energy into a volume of 47.9 cm3 that is at a gas pressure of 1.18×106Pa. In this short period of time the volume of the gas can be considered constant.

Treating the fuel-air mixture as a monatomic ideal gas at an initial temperature of 325 K, what is its temperature after ignition?

Answer 1

The temperature after ignition is 7859.565 K

Step-by-step explanation:

Here we have

Energy released = 1970 J

Volume of gas = 47.9 cm³ = 0.0000479 m³

Pressure of gas = 1.18 × 10⁶ Pa

Temperature of he gas = 325 K

From P·V = n·R·T

Therefore, n = PV/(RT) = (0.0000479 × 1.18 × 10⁶)/(8.3145× 325) = 2.09 × 10⁻² moles

For an ideal mono-atomic gas, the mono-atomic gas, the molar heat capacity at constant volume is given as

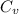`C_v` = 3/2 R ≈ 12.5 J K−1 mol⁻¹

Therefore we have

Heat released, ΔH = 1970 J = n ×
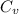`C_v`×(T₂ - T₁) = 2.09 × 10⁻² × 12.5×(T₂ -325)

T₂ = (1970 J)/(2.09 × 10⁻² × 12.5) + 325

= 7534.565 +325 = 7859.565 K

The temperature after ignition = 7859.565 K.

Answer 2

Temperature after ignition=7883.205 K

Step-by-step explanation:

The number of moles is,

n=PV/RT

=(1.18x10^6)(47.9x10^-6)/8.314(325)

= 0.0209 moles

a) In this process volume is constant

Q=U

=nCv.dT

dT= Q/nCv

=1970/(1.5x8.314)(0.0209)

= 7558.205 K

The final temperature is,

= 7558.205+325

= 7883.205 K