Answer:
11.6 m
Step-by-step explanation:
The intensity of sound is inversely proportional to the square of the distance from the source. If we denote intensity with I and distance with d,
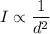
This can be resolved for any two situations as
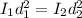
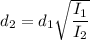
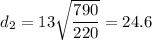
Therefore, you need to walk 24.6 - 13 m = 11.6 m away from the source.