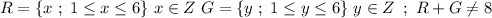Answer:
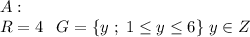
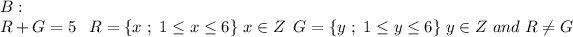
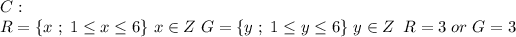
D:
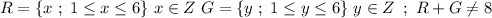
Explanation:
Let:
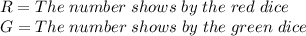
A:
This is easy, simply R=4, and we don't know the value of G, so:
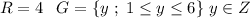
B: Be careful here, we know the numbers add to 5, so we don't know the exact value of R or G, because R could be 4 and G could be 1 or R could be 2 and green could be 3. However we can be sure that they can´t have the same value, because 5 is an odd number, if we add the same number to a number the result is always even: n+n=2n. So:
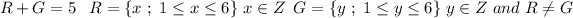
C: R is 3 or G is 3, that's the only thing we know, hence:
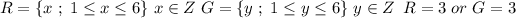
D: Similar to B, we only know that the sum of R and G isn't 8: