Answer:
≅ 1714N
Step-by-step explanation:
Start off by finding the total potential energy the person has at the top of the Tower.
PE = mass*g*Height
You can say the where the person stops is your reference level so at the 1.40m underwater there person has 0 potential energy. So the height is the Tower+1.40m
So for the person to stop 1.40m underwater they need to lose all of their energy to the water.
So work done by the water is the avg Force it exerts times the distance and the work done must equal the total enery the person has (which is the PE at the top of the tower). So:
Work = mgh
Work = F × d
F*d = m*g*h
m = 68kg
h = 2.20m + 1.40m = 3.60m
d = 1.40m
g = 9.8m/s²
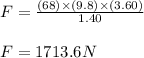
≅ 1714N