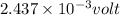Question

If a circular loop of wire of radius 19.7 cm is located in a region where the spatially uniform magnetic field perpendicular to the plane of the loop is changing at a rate of +2.0 ✕ 10−3 T/s, find the value of the induced EMF in this loop due to this changing magnetic field.

Answer 1

Magnitude of induced emf will be
`2.437* 10^(-3)volt`

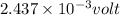
Step-by-step explanation:

We have given radius of the circular loop r = 19.7 cm = 0.197 m

So area of the circular loop
`A=\pi r^2=3.14* 0.197^2=0.1218m^2`

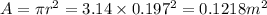
It is given that magnetic field is changing as
`2* 10^(-3)T/sec`

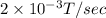
Emf induced in the circular loop is equal to
`e=(-d\Phi )/(dt)=-A(dB)/(dt)`

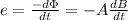
So emf induced will be equal to
`e=(-d\Phi )/(dt)=-0.1218*2* 10^(-3)=2.437* 10^(-3)volt`

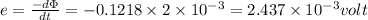
So magnitude of induced emf will be
`2.437* 10^(-3)volt`