Question

A 1.51 kg ball and a 1.97 kg ball are connected by a 1.63 m long rigid, massless rod. The rod is rotating clockwise about its center of mass at 38 rpm. What torque will bring the balls to a halt in 7.5 s? (Give an absolute value of torque.)

Answer 1

`T = 1.205\,N\cdot m`

Step-by-step explanation:

Needed torque can be estimated by means of the Theorem of Angular Momentum Conservation and Impact Theorem. The center of mass of the system is:

`\bar r = ((0\,m)\cdot (1.51\,kg)+(1.63\,kg)\cdot (1.97\,kg))/(1.51\,kg+1.97\,kg)`

`\bar r = 0.923\,m`

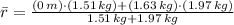
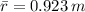
Let assume that both masses can be modelled as particles, then:

`[(1.51\,kg)\cdot (0.923\,m)^(2) + (1.97\,kg)\cdot (0.707\,m)^(2)]\cdot (38\,(rev)/(min) )\cdot ((2\pi\,rad)/(1\,rev) )\cdot ((1\,min)/(60\,s) ) -T\cdot (7.5\,s) = 0\,(kg\cdot m^(2))/(s)`

The torque needed to stop the system is:

`T = 1.205\,N\cdot m`