Question

While Layla gets paid significantly more per hour than Olivia, she is reducing the overall cost of this system. How much money is being saved per hour by utilizing the new technician, Layla?

Answer 1

Solution and Explanation:

Olivia

Average arrival rate, λ = 2.1 problems per hour

Average service rate, μ = 2.9 problems per hour

Assume Poisson arrival and exponential service time in order to make use of the M/M/1 queue formula.

The average number of computes not available (i.e. either waiting for repair or getting repaired), Ls = λ / (μ - λ) = 2.1 / (2.9 - 2.1) = 2.625

Total cost per hour = Ls multiply $17 + $20 = 2.625 multiply 17 + 20 = $64.625

Layla

Average arrival rate, λ = 2.1 problems per hour

Average service rate, μ = 3.6 problems per hour

Ls = λ / (μ - λ) =
`2.1 /(3.6-2.1)=1.40`

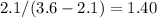
Total cost per hour = Ls multiply $17 + $29 = 1.40 multiply 17 + 29 = $52.8

So,

cost saved per hour = 64.625 minus 52.8 = $11.825