Question

The force on a particle is directed along an x axis and given by F = F0(x/x0 - 1) where x is in meters and F is in Newtons. If F0 = 1.5 N and x0 = 4.5 m, find the work done by the force in moving the particle from x = 0 to x = 2x0 m.

Answer 1

W = 17.5J.

Step-by-step explanation:

Given that F = Fo(x/(xo – 1)), Fo = 1.5N and xo = 4.5m

Substituting the given values into the equation for F we have

F = 1.5x /(4.5 –1 ) = 1.5x/3.5 = 0.43x

F = 0.43x

Workdone dW = F×dx (infinitesimal workdone).

So to get the workdone,

W = ∫Fdx = ∫0.43x dx = 0.43x²/2

So the workdone in moving the particle from x1 = 0 to x2 = 2xo = 2×4.5 = 9.0m is

W = 0.43/2 ×(9² – 0²) = 0.215×81 = 17.5J

Answer 2

Answer: The work done is 28.9 j

Step-by-step explanation:

The work is defined as a force doing a movement, and it can be calculated as W = F*d

The force is:

F = 1.5N*(x/(4.5m - 1m)) = (1.5)N*x/3.5m

the distance that d = 2x0 = 2*4.5m = 9m

But the force changes in function of x, so we must do a integration:

`\int\limits^9_0 {(1.5N*x)/(3.5m) } \, dx`

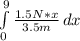
Where i used d as the integral of dx betwen 0m and 9m, so the only thing inside the integral is the equation for the force.

this integral is equal to:

W = (2.5N*x^2)/(2*3.5m) valued between x = 0m and x = 9m

W = (2.5*9^2)/7 J = 2.5*81/7 J = 28.9J