Question

A small current element carrying a current of I = 1.00 A is placed at the origin given by d → l = 4.00 m m ^ j Find the magnetic field, d → B , at the locations specified. Enter the correct magnitude and select the direction from the list. If the direction is negative, indicate this by entering the magnitude as a negative number. What is the magnitude and direction of d → B on the x ‑axis at x = 2.50 m ? magnitude: T Direction: ^ k ^ j ^ i What is the magnitude and direction of d → B on the z ‑axis at z = 5.00 m ?

Answer 1

the magnitude and direction of d → B on the x ‑axis at x = 2.50 m is -6.4 × 10⁻¹¹T(Along z direction)

the magnitude and direction of d → B on the z ‑axis at z = 5.00 m is 1.6 × 10⁻¹¹T(Along x direction)

Step-by-step explanation:

Use Biot, Savart, the magnetic field

`d\bar{B}=(U)/(4\pi ) \frac{i(d\bar{l}* r)}{r^2}`

Given that,

i = 1.00A

d → l = 4.00 m m ^ j

r = 2.5m

Displacement vector is

`\bar{r}=x\hat i+y\hat j+z \hat k\\`

`\bar{r}= (2.5m) \hat i +(0m)^2 + (0m)^2`

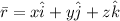
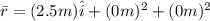
=2.5m

on the axis of x at x = 2.5

`r = √((2.5)^2 + (0)^2 + (0)^2)`

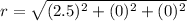
r = 2.5m

And unit vector

`\hat r =\frac{\bar{r}}{r}`

`= (2.5 \hat i)/(2.5)\\\\= 1\hat i`

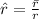
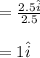
Therefore, the magnetic field is as follow

`d\bar{B}=(U)/(4\pi ) \frac{i(d\bar{l}* r)}{r^2}`

`d\bar{B} = ((10^-^7)(1)(4*10^-^3j* i)/((2.50)^2) \\\\d\bar{B} = -6.4*10^(-11) T`

(Along z direction)

B)r = 5.00m

Displacement vector is

`\bar{r}=x\hat i+y\hat j+z \hat k\\`

`\bar{r}= (5.00m) \hat i +(0m)^2 + (0m)^2`

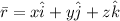
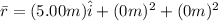
=5.00m

on the axis of x at x = 5.0

`r = √((5.00)^2 + (0)^2 + (0)^2)`

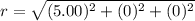
r = 5.00m

And unit vector

`\hat r =\frac{\bar{r}}{r}`

`= (5.00 \hat i)/(5.00)\\\\= 1\hat i\\`

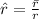
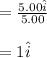
Therefore, the magnetic field is as follow

`d\bar{B}=(U)/(4\pi ) \frac{i(d\bar{l}* r)}{r^2}`

`d\bar{B} = ((10^-^7)(1)(4*10^-^3j* i)/((5.00)^2) \\\\d\bar{B} = 1.6*10^(-11) T`

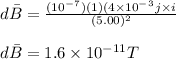
(Along x direction)