Question

Resistor A has twice the resistance of resistor B. The two are connected in series and a potential difference is maintained across the combination. The rate of thermal energy dissipation in A is: 1. one fourth that in B 2. the same as that in B 3. four times that in B 4. half that in B

Answer 1

The thermal energy dissipated in A would be twice that in B

Step-by-step explanation:

Resistor B (RB)= R

Resistor A (RA)= 2 R

When they are connected in series the equivalent Resistance in the circuit would be;

Equivalent resistance = RA +RB = R + 2 R = 3 R;

From ohms law I = V/R

I = V/3 R

Now the thermal energy is the power dissipated by the circuit and can be obtained thus;

P =
`I^(2)R`

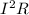
Then,

`P_(A) = ((V)/(3R)) ^(2) *2 R\\\\P_(A) = (V^(2) )/(9R^(2) ) *2R\\\\P_(A) = (2)/(9)( (V^(2) )/(R)) \\\\P_(B) = ((V)/(3R)) ^(2) * R\\\\P_(B) = (V^(2) )/(9R^(2) ) *R\\\\P_(B) = (1)/(9)( (V^(2) )/(R))`

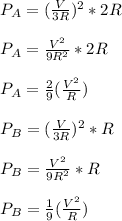
Therefore Pa : Pb = 2: 1, this means that the thermal energy dissipated in A would be twice that in B