Question

The length of time needed to complete a certain test is normally distributed with mean 35 minutes and standard deviation 15 minutes. Find the probability that it will take less than 6 minutes to complete the test. a) 0.9867 b) 0.9734 c) 0.0133 d) 0.0266 e) 0.5000 f) None of the above

Answer 1

The probability that it will take less than 6 minutes to complete the test is 0.0266.

Explanation:

We are given that the length of time needed to complete a certain test is normally distributed with mean 35 minutes and standard deviation 15 minutes.

Let X = length of time needed to complete a certain test

SO, X ~ N(
`\mu = 35,\sigma^(2) = 15^(2)`)

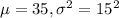The z-score probability distribution is given by ;

Z =
`(X-\mu)/(\sigma)` ~ N(0,1)

where,
`\mu` = mean time to complete the test = 35 minutes

`\sigma` = standard deviation = 15 minutes

The Z-score measures how many standard deviations the measure is away from the mean. After finding the Z-score, we look at the z-score table and find the p-value (area) associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X.

Now, the probability that it will take less than 6 minutes to complete the test is given by = P(X < 6 minutes)

P(X < 6) = P(
`(X-\mu)/(\sigma)` <
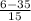`(6 - 35)/(15)` ) = P(Z < -1.933) = 1 - P(Z
`\leq` 1.933)

= 1 - 0.9734 = 0.0266

The above probability is calculated using z table by looking at value of x = 1.933 which will lie between x = 1.93 and x = 1.94 in the z table which have an area of 0.9734.

Therefore, probability that it will take less than 6 minutes to complete the test is 0.0266.