Answer:
E = 1,873 10³ N / C
Step-by-step explanation:
For this exercise we can use Gauss's law
Ф = E. dA =
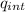 / ε₀
/ ε₀
Where q_{int} is the charge inside an artificial surface that surrounds the charged body, in this case with the body it has a spherical shape, the Gaussian surface is a wait with radius r = 1.35 m that is greater than the radius of the sphere.
The field lines of the sphere are parallel to the radii of the Gaussian surface so the scald product is reduced to the algebraic product.
The surface of a sphere is
A = 4π r²
E 4π r² = q_{int} /ε₀
The net charge within the Gauussian surface is the charge in the sphere of q1 = + 530 10⁻⁹ C and the point charge in the center q2 = -200 10⁻⁹ C, since all the charge can be considered in the center the net charge is
q_{int} = q₁ + q₂
q_{int} = (530 - 200) 10⁻⁹
q_{int} = 330 10⁻⁹ C
The electric field is
E = 1 / 4πε₀ q_{int} / r²
k = 1 / 4πε₀
E = k q_{int}/ r²
Let's calculate
E = 8.99 10⁹ 330 10⁻⁹/ 1.32²
E = 1,873 10³ N / C