We know that, the area of a square with side being s, is given by s², so if we here assume our side of square whose area is (16/36) sq. foot being s, so we will be having :
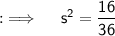
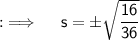
But, as length can never be -ve, so we will be taking only +ve length, and if we solve further for s, it will yield ;
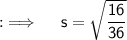
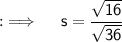
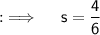
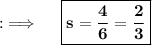
Well, you might be thinking that (2/3)² willn't give (16/36) rather it will give (4/9), so for this, I'm telling that (2/3) ≈ 0.66666...7 and (4/6) ≈ 0.66666...7, so it's just the same thing and also, (16/36) and (4/9) are just too the same thing, dividing the numerator and denominator of (16/36) will just lead to (4/9) as same as (2/3)²