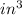Answer:
The maximum volume is: 11.52 *10.52*2.74 = 332.06
Explanation:
Let x is the side of the square in inches.(x >0)
The volume of the resulting box when the flaps are folded up can be expressed as:
V = x (17 -2x)(16-2x)
= (17x -2
 )(16-2x)
)(16-2x)
=
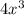 - 66
- 66
 + 272x
+ 272x
To find the value of x which yields the maximum of volume (V), take the first derivative of this equation and set it equal to zero.
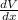 = 12
= 12
 - 66x + 272
- 66x + 272
Solve 12
 - 132x + 272 = 0
- 132x + 272 = 0
<=> x = 2.74
The dimensions of the box are:
Length: (17 -2x) = (17 -2*2.74) = 11.52
Width: (16-2x) = (16-2*2.74) = 10.52
High: x = 2.74
So the maximum volume is: 11.52 *10.52*2.74 = 332.06