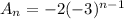Answer:
1. Geometric sequence
2.
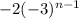 ;
;
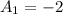
3.
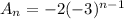
Explanation:
The sequence is Geometric.
For the sequence to be Geometric , then there must exist a common ratio
check:
6/-2 = -18/6 = 54/-18 = -3
The recursive formula for the sequence is :
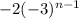 ;
;
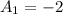
To find the explicit formula:
The formula for the nth term of a Geometric sequence is given as :
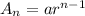
where :
a = first term
r = common ratio
so , substituting the values into the formula , we have :
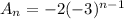
therefore : the explicit formula =