Product of n and p is 32 out of available options ! correct option is (E) 32
Explanation:
Here we have , n and pare positive integers and 4n/P = V1024, then we need to find the product of n and p . Let's find out:
According to question we have following equation
⇒
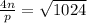
⇒
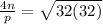
⇒
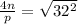
⇒
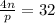
⇒
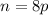
Now , product of n and p is :
⇒
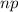
⇒
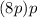
⇒
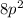
Value of p is positive integer So , Let f(p)=
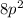 :
:
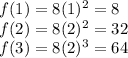
Hence , Product of n and p is 32 out of available options ! correct option is (E) 32 .